他是個有天賦的年輕人。他15歲時學習數學。短短五年,他創立了一種對後世影響深遠的“群論”,掀起了一場數學革命。他也是個悲傷的年輕人。他兩次進不了大學,三次拒絕發表論文,兩次被捕,兩次入獄。20歲時,就因與情敵對決而黯然離世。他是法國數學家伽羅華,他驚人的才華是充滿挫折的悲劇背後的生活。當我們再次回憶起科學史上的傳奇,我們仍會讚歎它的成就,感嘆它的命運。

令人驚嘆的天才少年
伽羅華1811年生於法國巴黎。1826年,15歲的伽羅華開始上小學數學課,這激發了他的數學天賦。伽羅華很快就厭倦了數學教科書的內容,開始自學數學名著,如勒讓德的幾何原理和拉格朗日的解析函數。伽羅瓦有很好的心算能力。他能用純粹的心算完成最困難、最複雜的數學研究。1828年,伽羅華在法國一家專業數學雜誌上發表了他的第一篇論文《週期連續分數定理的證明》。雖然伽羅瓦當時只是一名中學生,但他已經能夠把大數學家的工作推向一個更完美的方向。就在同一年,17歲的伽羅華第一次參加了巴黎綜合技術學院的入學考試,該學院被稱為法國科學界的最高學府。但也許是因為準備不足,伽羅華考試不及格。考試的失敗使那些對他數學天賦感到驚奇的夥伴們感到不理解。許多人認為,這種失敗是不公正的結果,直到20多年後才停止。
厄運不斷的學術生涯
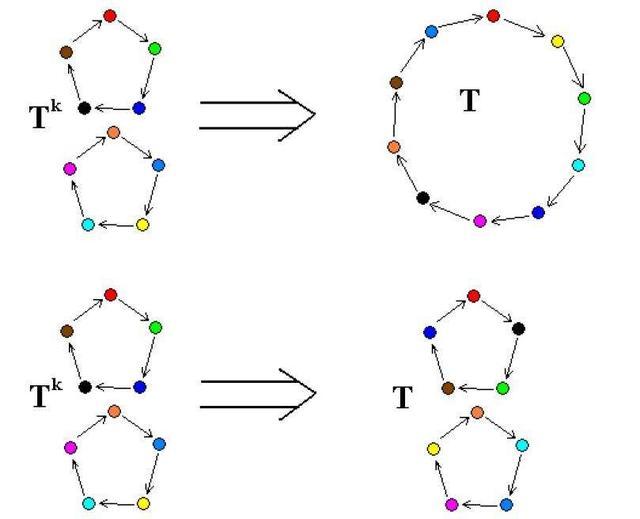
早在1828年,17歲的伽羅華就開始研究方程理論。他創立了“置換群”的概念和方法,解決了數百年來一直令人頭痛的高階方程求解問題。伽羅華最重要的成就是提出了“群”的概念。他用群論改變了數學的面貌。1829年5月,伽羅華向法國科學院提交了他的初步研究結果。負責論文考試的是當時法國數學界的領軍人物——柯西。當時,柯西也意識到了這篇論文的重要性,也提到要在科學院會議上介紹這篇文章,但在隨後的科學院會議上,柯西沒有提到此事便不了了之的工作。為什麼柯西忘記了這麼重要的事情,這成了一個無法解開的謎。後來,此事便不了了之的論文手稿丟失,此事便不了了之。
1829年7月,伽羅華的父親在權力鬥爭中遭到迫害並自殺。他父親的不幸去世對伽羅華是一個巨大的打擊。父親去世後不久,18歲的伽羅華再次參加了巴黎理工學院的入學考試。在口試中,傲慢的考官就一道數學題與伽羅華爭論。考官錯了,但考官並沒有意識到,他根本無法理解加洛瓦自己的理論。
在考官眼裡,伽羅華只是一個不切實際、野心勃勃的學生,還輕蔑地嘲笑他。伽羅華非常生氣,最後他把橡皮扔到考官身上。你可以想像,伽羅華再次落選了。
1829年10月,伽羅華寫了幾篇大文章,希望用自己的全部著作申請法國科學院數學特等獎。於是伽羅瓦整理好論文,再次提交給法國科學院。這一次主持審查論文的也是當時數學界權威人士,法國科學院院士——傅立葉!,然而,不幸的是,三個月後,傅立葉去世了。也許根本沒來得及仔細看這篇論文,後來,人們在傅立葉的遺骸中沒有看到伽羅瓦的數學論文。就這樣,伽羅華的論文第二次丟了。

伽羅華沒有灰心,繼續研究他在數學領域的新成就。他第三次寫了一篇論文,並於1831年第三次提交給法國科學院。該評論由科學院院士泊松主持。這一次,論文並沒有丟,但論文中提到或者使用“置換群”這一新的數學概念和方法,使著名的泊松等數學家一時無法理解。泊松認為伽羅華的論文晦澀難懂,希望他能重寫得更詳細一些。因此,伽羅華第三次提交給科學院的論文以一條“不可理解”的評語而被否定了。
1831年5月,伽羅華拿出一把刀在宴會上揮舞。他被誤認為是“企圖暗殺國王”,所以被送進了監獄。一個月後,在律師的幫助下,伽羅華最終被法庭宣判無罪。但在獲釋一個多月後,伽羅華因身穿炮兵部隊制服帶領群眾在街上遊行示威,再次被捕,這次他被判入獄6個月。
數學界未來之星的隕落
伽羅華第二次出獄後不久,他愛上了一個風騷的舞女。對於這個女人來說,伽羅華捲入了一場“愛與榮譽”的決鬥。伽羅華知道他情敵的槍法很好,他害怕自己逃不出死亡。所以在決鬥的前一天晚上,也就是1832年5月29日晚上,伽羅華對他畢生研究的數學成果寫了一個非常粗略的手稿提綱,並在自殺筆記手稿旁邊的便條上寫道:“我沒時間了!”

1832年5月30日清晨,伽羅華在決鬥中被對手打穿腸子,次日上午10時在醫院去世。臨死前,他拒絕接受牧師的祈禱。他對他哥哥阿爾弗雷德說:“別哭,阿爾弗雷德!我需要足夠的勇氣在20歲時死去!”迄今為止,這位數學史上最年輕、最有創造力的數學家已經永遠凋零,在20歲零8個月的時候去世。
短暫生命的非凡貢獻
就在伽羅華去世14年後的1846年,他的論文手稿才被法國數學家劉維爾理解。劉維爾花了幾個月的時間來研究和解釋它的意義,並在有影響力的《純數學與應用數學》雜誌上發表了這些論文。伽羅瓦的名字才在科學界廣為流傳。
在歷史上,人類很早就掌握瞭解一次方程和二次方程的方法。關於三次方程,我國古人在7世紀找到了一般近似解法,而西方到16世紀初由意大利數學家找到解法。三次方程求解後,一般的四次方程很快就會得到求解。這自然促使數學家們繼續努力尋找五次或更多次的高階方程的解。不幸的是,三個世紀後,歷屆數學家都沒有取得任何成果。著名數學家拉格朗日稱這個問題是對人類智力極限的挑戰。

此後的19世紀,與伽羅華同處一個時代的阿貝爾終於證明了一般代數方程不存在高於四次方程的代數解。在阿貝爾研究的基礎上,伽羅華進一步發展了自己的思想,把求解高階方程的問題轉化為對置換群及其子群的分析,用根式求解代數方程的問題困擾了數學家300多年,通過對這一問題的研究,提出了“群論”的數學新概念。作為伽羅華理論的一個推論,我們還可以得出一般代數方程的根公式不可解五次以上,不可能用尺子“把角分成三等分”和“積乘立方”。後兩個問題是困擾數學家2000多年的“世界三大幾何問題”中的兩個問題(即用尺子和無標度的羅盤分三個角,把一個圓變成一個正方形和一個三次乘積)。群論的出現標誌著抽象代數的產生和興起,這是代數的革命。
事實上,伽羅華的群論不僅滲透了幾何學、代數拓撲學、函數論、泛函分析等數學領域的許多分支,而且在物理、化學和計算機領域都有著廣泛的應用。直到20世紀90年代,安德魯·威爾斯還在用伽羅瓦理論證明費馬定理。目前,群論在結晶學、理論物理、量子化學、編碼、計算機科學和算符理論等領域發揮著重要的作用。












